HOME > 徒然「光」基礎講座 > 膜厚測定・干渉分光法とは: 5. 古典的な解析法
膜厚測定・干渉分光法とは: 5. 古典的な解析法
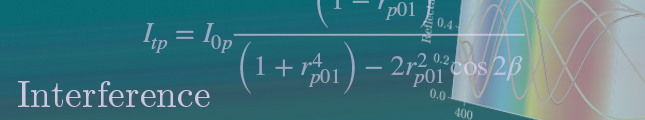
5. 古典的な解析法
分光スペクトルに重畳する干渉フリンジを利用した膜厚測定は,古くから行われています. 現在ではコンピューターを使ったスペクトルフィッティング解析が一般的ですが,コンピューターがない時代には,屈折率を既知の固定値として簡略化した計算法で膜厚を求めたり,干渉の特異的な波長を利用するといった計算上の工夫をして屈折率を求めたりしていました. ここでは,それら古典的なスペクトル解析法の概要について説明します.
5.1 古典的な解析法 1
最初に紹介する解析法は,いろいろな仮定をおいて計算を簡略化して膜厚を求める方法です. 具体的には,屈折率を仮定して干渉フリンジのピークとバレーの数から膜厚に換算する方法で,一般にピークバレー法( PV 法)と呼ばれています.
ここでは,BK7基板(厚さ: 1mm ) 上の TiO2 膜(厚さ: 0.813µm ) をサンプルにして,入射角:5°で測定した反射率スペクトルの例を示します. 図5-1 は,(a) がBK7基板上の TiO2 膜サンプルにおける光の透過と反射のようす, (b) が入射角:5°の反射率スペクトル例で,解析波長範囲を 400 ~ 1000nm にしてピークとバレーをマークしてあります.
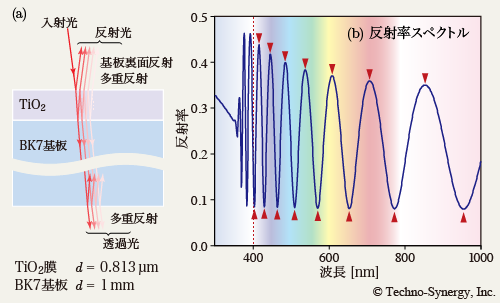
サンプルに入射した光は,膜表面で一部の光が反射し残りが透過します. 膜-基板界面に到達した光は一部が反射し残りが透過します. このように,光は界面に出会う度に一部が反射し残りが透過する多重反射を繰り返します. 私たちが観測する反射光は,膜の多重反射光と基板裏面からの反射光を全て足したもので,材料に吸収がなければ透過光を除いた残りの入射光です.
PV 法では,解析波長範囲を決めて,その波長範囲にあるピークとバレーの数,および解析波長範囲の両端のピーク / バレーの波長を使い (5-1) 式で膜厚を求めます.

ここで, d は膜厚, n は膜の屈折率, θi は入射角, λ2 は短波長側のピーク / バレー波長, λ1 は長波長側のピーク / バレー波長です. 膜の屈折率は,解析波長範囲内で一定と仮定し,既知の値として入力する必要があります.
さて, PV 法は色々な仮定のもとで膜厚を計算する簡便法ですので,いくつかの問題点があります. まず,屈折率が既知という前提から,屈折率が未知の膜は扱えませんし,屈折率値に誤差があると算出される膜厚にも同程度の誤差が入ります. また,解析波長範囲内で屈折率が一定という仮定は,解析できる膜材料や解析できる波長範囲にかなり厳しい制約が生じることになります. 2 つ目は,解析にはピーク / バレー数がある程度必要なことから,膜厚が薄くピーク / バレー数が少ない膜サンプルには適用できないことです. 例えば,図5-1 の条件では,膜厚 200nm でくピーク / バレー数が4になり,それより薄い膜への適用は難しいと考えられます. また,(5-1) 式から分かるように,膜以外の光物性情報,例えば基板の屈折率などは無視されます. つまり,単層膜にしか適用できず,多層膜は解析できません. その他,屈折率を一定値としているので,基本的に吸収膜には適用できず,光学異方性がある膜は扱えないといった問題もあります.
干渉フリンジの周期性から膜厚を算出する方法として,フーリエ変換を用いる方法もポピュラーです. フーリエ変換法も,屈折率を既知として解析する流儀をとっていて,基本的に, PV 法と同様にサンプルの光物性を無視する簡易的な膜厚解析法だと言えます.
5.2 古典的な解析法 2
様々な構成の多層薄膜サンプルの光学特性は, 各層の光学定数と膜厚からフレネル係数 ( Fresnel equation ) の計算によって求めることができます. しかし, 逆に測定スペクトルから各層の膜厚と光学定数を解析的に求めることは, 単層膜といえども困難です. 理想的な薄膜に対して, 関係するパラメーターは屈折率 n , 消衰係数 κ , そして膜厚 d の三つですが,n , κ は波長の関数なので問題は複雑になります.
そのため, 単純な解を持つ特殊な場合に限って, 光学定数の決定が可能です. つまり, 一般的には, 干渉スペクトル中の, (5-2) 式( 「2.1 薄膜干渉とは」参照)の干渉条件を満たすとびとびの波長(ピークとバレー)における透過率または反射率から, 屈折率を求める方法がとられます.
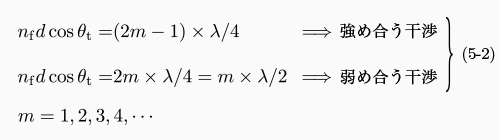
ここでは, 基板と膜がともに透明な単層膜を例に, 極大透過率 TM と極小透過率 Tm を利用して光学定数を求める包絡線法 [3] について説明します.
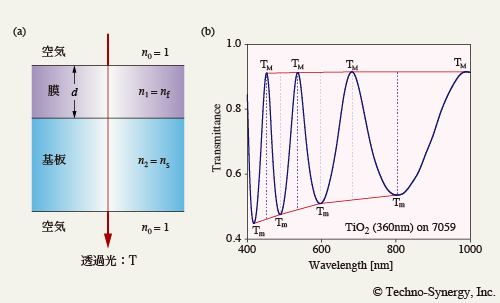
解析モデル, 透過率シミュレーションともに垂直入射を仮定しています. 膜の屈折率 n f が基板の屈折率 n s より大きい場合, 透過光における薄膜の干渉は, n f d = 2m × λ / 4 ( m = 1, 2, 3, ・・・ ) を満たす波長で強め合って極大透過率 TM となり, n f d = (2m - 1) × λ / 4 ( m = 1, 2, 3, ・・・ ) を満たす波長で極小透過率 Tm をとります. そのため, 膜の透過率スペクトルは, 図5-1(b) のような, 干渉の次数 m に応じた複数の TM と Tm の間を振幅する形状を示します.
ここで, TM 同士, Tm 同士をそれぞれ直線で結ぶと, 近似的に干渉振幅波形の包絡線と見なすことができ, 包絡線上の透過率値を用いることによって, 任意の波長で一対の TM と Tm を得ることができます. 膜が透明 ( κ = 0 ) な場合, ある波長における TM と Tm は, 基板屈折率 n s と膜屈折率 n f を用いて次式で与えられます.
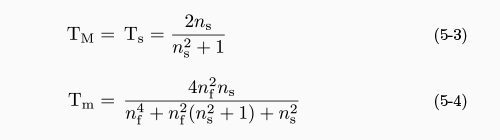
なお, Ts は基板単体の透過率です. (5-3) 式と (5-4) 式から,膜の屈折率 n f を次のように求めることができます.
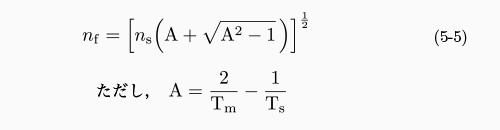
n f < n s の場合には, 薄膜-基板界面での反射位相が π ずれるため, 上式の TM と Tm を入れ替えて計算します.
包絡線法は, 微弱な吸収を持つ膜にも適用可能で, 光通信帯などの吸収が少なく屈折率の波長分散が小さい波長領域では有効な屈折率算出法です. しかし, 直線近似した包絡線を基に計算を行うため, 吸収があり屈折率分散が大きな波長領域では, TM と Tm の値が曖昧になりやすく誤差が生じやすいという問題があります. また,屈折率決定精度を上げるためには,干渉フリンジを密にする必要があり薄膜には適用できません.
ここで示したような透過率の極大値 / 極小値を利用した屈折率決定法には, 種々のバリエーションがあります. それらの詳細は, 文献 [3] ~ [6] をご参照ください.
[3] J. C. Manifacier, J. Gasiot and J. P. Filland: "Simple method for determination of the optical constant n, k and the thickness of weekly absorbing thin films", J. Phys. E.: Sci. Inst. 9 (1976) pp.1002-1004.
[4] H. A. Macleod: "Thin-Film Optical Filters" (Macmillan, New York, Second edition, 1986), H. A. Macleod (著), 小倉繁太郎他 (訳) :「光学薄膜」, 日刊工業新聞社 (1989).
[5] 小檜山光信:「光学薄膜の基礎理論」, オプトロニクス社 (2003).
[6] 李正中:「光学薄膜と成膜技術」, アグネ技術センター (2003).





