6.1 可視領域における誘電体材料の正常分散

図6-1 にいくつかの重要な誘電体材料の屈折率分散を示します． 広い波長範囲を1つの図に収めるために横軸は log λ [µm] でプロットしてあります．

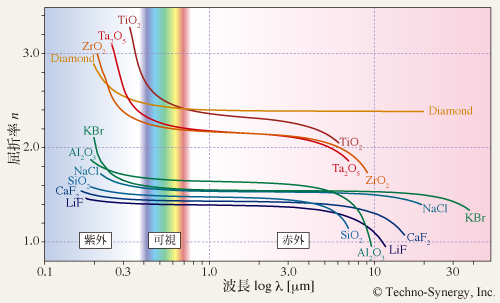
誘電体材料の種類によって屈折率の高さや屈折率分散の形状はまちまちですが，実は，波長に対する大きな形状変化はどの材料も似通っていることが分かります． つまり，紫外領域では，短波長側に向かって屈折率が増大し，赤外領域では長波長側に向かって屈折率が減少していて，透明な可視領域では短波長から長波長に向かって屈折率が徐々に低下する正常分散を示します 実は，この波長分散形状に，光物性の本質が隠されているのです．
紫外領域には光の電場に電子が応答することで生まれる電子分極の吸収帯があり，赤外領域には光の電場に対してイオンが応答することで生まれるイオン分極の吸収帯があります． その状態をモデル的に再現してみましょう．
図6-2 電子分極の吸収帯とイオン分極の吸収帯を Lorentz振動子 を使ってモデル化した例です（ Lorentz 振動子については後ほど説明します）． 図6-1 に合わせて横軸は log λ [µm] でプロットしてあります．

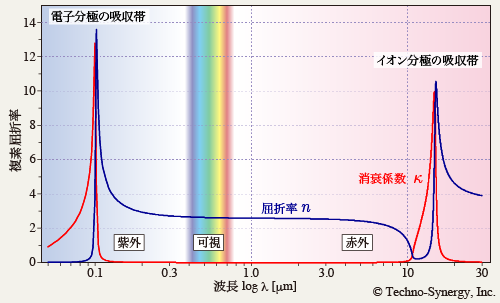
紫外領域の波長 0.1 µm の辺りに電子分極による消衰係数 κ のピークがあり， κ が 0 で透明な可視領域を挟んで，赤外領域の波長十数ミクロンの辺りにイオン分極による κ のピークがります． 言い換えると，可視領域は電子分極の吸収バンドとイオン分極の吸収バンドの間のバンドギャップに位置するため，吸収がなく透明なのです．
吸収帯における消衰係数 κ の分散形状，屈折率 n の分散形状がどうしてこのような形になるかは後ほど明らかになります． 屈折率 n と消衰係数 κ は互いに独立に決まるものではなく，光の電場に物質中の電荷が応答することで必然的に両者の関係が決まります． これを因果律といいます． 図6-1 に示した屈折率の独特な分散カーブは，電子分極の吸収とイオン分極の吸収が存在することで，必然的にできるカーブ形状なのです．
図6-2 のように単純化された屈折率分散モデルでも，図6-1 に示した誘電体材料の基本的な正常分散特性を十分に説明できることが分かります．

また，図6-1 で分かるように，赤外領域のイオン分極による吸収の影響は，通常，波長 1µm よりも長い赤外領域に限定されます． ですので，可視領域における屈折率の正常分散形状は，紫外領域にある電子分極の吸収によって決定されていると言って差し支えありません． ここからは，図6-2 に示した紫外領域の電子分極による吸収帯に絞って見ていくことにします．

6.2 光の電場に対する物質の応答

光は電磁波であり，互いに直交する正弦波状の電場 E と磁場 B が，光速 c で進む横波です． 光の電場と磁場のうち磁場の方は，物質が磁性体でない限り物質に影響を与えません． つまり，光は光の周波数で振動する交流電場と考えてよいのです．
さて，誘電体に光が入射した状態を想像してみましょう． 誘電体内の原子は重い原子核と軽い電子で構成されており，光の電場に応答して軽い電子だけが動きます． この原子核に対して電子が移動して電荷が偏る現象を分極と呼びます． 分極した電子と原子核はプラス / マイナスで引き合いますから，両者の間にはバネのような復元力が働きます． そのため，入射した光の交流電場に軽い電子がクーロン力を受けて原子核を中心にして振動することになります． この光の電場に対する電子の応答は，バネの運動に置き換えられます． さらに，振動する電子（荷電粒子）は光を放出します． これを電気双極子放射と呼びます． 詳細は省きますが，入射してきた光と電気双極子放射が足し合わされた結果が，光の透過，屈折，反射といったマクロな光学現象を生んでいるのです．

こうした光の電場に対する物質応答大きさは誘電率で表され，誘電率の分散はバネの運動方程式によって定式化されます． その代表が， Lorentz 振動子（ Lorentz oscillator ）です． Lorentz 振動子は， Lorentz モデルとも呼ばれます．

Lorentz 振動子は, 正電荷を持つ原子核と負電荷を持つ電子がバネで束縛されているとする古典的なモデルで，量子効果は考慮されません. 光の電場振動 E = E₀ exp (iωt) に対して, 質量の大きい原子核は動かず, 電子だけが粘性流体中を振動する物理モデルを仮定しています. 光の電場などの外場から与えられるエネルギーと粘性抵抗で失われるエネルギーが釣り合って安定に振動します. つまり，光が当たっている間は振動子続けますが，光がなくなると振幅が減衰して元の分極していない原子に落ち着きます． このような振幅の減衰を伴う振動系を，減衰振動子 ( damped oscillator ) と呼びます. Lorentzモデルの運動方程式は次式で与えられます.

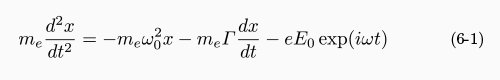
ここで m_e と e は, それぞれ電子の質量と電荷です. 右辺第2項は粘性流体中の粘性抵抗によるエネルギー損失を表しており, 運動速度が遅い場合は速度に比例します. Γ は粘性抵抗の比例係数で, 減衰係数 ( damping coefficient ) と呼ばれます. 右辺第1項は, 光の電場によって移動した電子がフックの法則 ( F = -k_F x ) に従って復元することを表しています． ここで， ω₀ はバネの共鳴角振動数で, F = -k_F x から ω₀ = (k_F / m_e)^1/2 と与えられます. 右辺第3項は, exp ( iωt ) で振動する光の交流電場から受けるクーロン力です． (6-1) 式は, 光の交流電場によって電子が e E₀ exp ( iωt ) で加振される減衰振動子の運動方程式です.
図6-3 は Lorentz モデルから計算される誘電率の分散，すなわち誘電関数の例です． 挿入図は，強制的に加振される減衰振動子の物理イメージ図です．

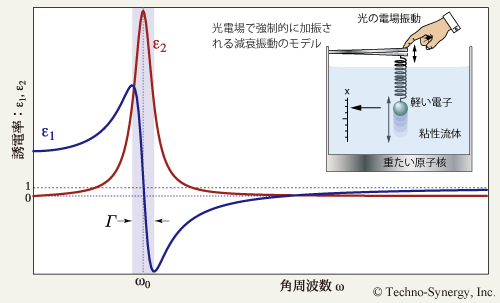
誘電率の実部 ε ₁ は，電場にって分極する度合い（電場が電荷及ぼす力）を表し，虚部 ε ₂ は誘電損失とも呼ばれ，光の共鳴吸収の強さを表します． 誘電率の実部 ε ₁ と虚部 ε ₂ は，互いに独立ではなく，物質中の電荷が入射光の電場に対してバネのように振動応答することによって決まる因果律で結びつけられています． この ε ₁ と ε ₂ の関係は，クラマース・クローニッヒの関係式 （ Kramers-Kronig relation ） で表されます．

6.3 電子分極による吸収帯

図6-2 に示した紫外領域の電子分極による吸収帯は，紫外領域の適当な波長に配置された Lorentz 振動子によって作り出されています． 図6-4 は，図6-2 の Lorentz 振動を横軸エネルギー [eV] で拡大して描き直した図です．

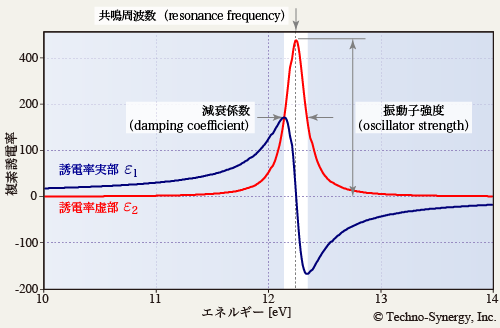
光の共鳴吸収の強さを表す誘電損失 ε₂ は，スペクトル横軸をエネルギーリニアにすると，共鳴周波数を中心に対象な形になります． この ε₂ の分布形状を Lorentz 関数と呼びます． Lorentz 関数は，共鳴吸収が極大になる共鳴周波数（ resonance frequency ） ，共鳴吸収の極大値である振動子強度（ oscillator strength ）， Lorentz 関数の広がり幅を表す減衰係数Γ ( damping coefficient ) の3つのパラメーターでその形状が決定されます． Lorentz 関数の広がり幅を表すダンピングは，(6-1) 式で示した粘性流体中の粘性抵抗の比例係数 Γ で，振動子強度の半値全幅です．

物質の屈折率 n は，真空中の光速度 c と物質中の光速度（位相速度）の比 n ≡ c / v と定義されます． 誘電体など非磁性体では，透磁率を µ = µ₀ としてよいので，屈折率 n は，物質の誘電率 ε _p を真空中の誘電率 ε ₀ で割って無次元化した比誘電率 ε だけを含む簡単な式で表されます．

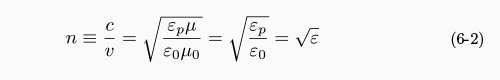
(6-2) 式は複素数に対しても成り立ちます． つまり，誘電関数と屈折率の波長分散は変換可能です． 図6-3 の誘電関数を，複素屈折率分散に変換して，横軸波長 [µm] にしてプロットしたのが図6-4 です．

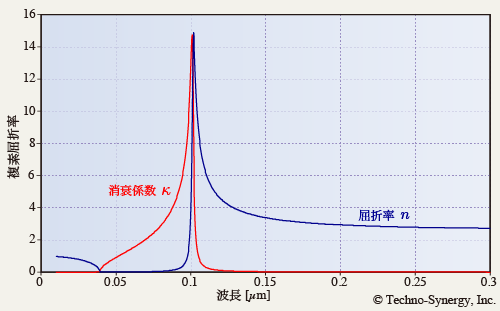
スペクトル横軸がエネルギーに比例する場合に左右対称な Lorentz 振動子の誘電関数を，縦軸を複素屈折率，横軸を波長に変換すると，吸収帯における不思議な消衰係数分散のカーブ形状，吸収帯の長波長側で正常分散する屈折率の分散カーブ形状が作り出されることが分かります．

誘電関数や屈折率分散の基本的な形状は， Lorentz 振動子で記述できることが分かりました． 次回第7回は，誘電関数を記述する上で必要な Drude モデルやその他の振動子モデルなどを紹介していきます．